含水层隧道渗流场理论解与数值解结果对比
案例说明
隧道外水压力是隧道施工的重要参数。考虑有限含水层中的单孔圆形带衬砌隧道,研究含水层厚度、隧道埋深、注浆圈渗透性、多孔泄压等对隧道渗流的影响,并与部分对应的理论解和ABAQUS对比。
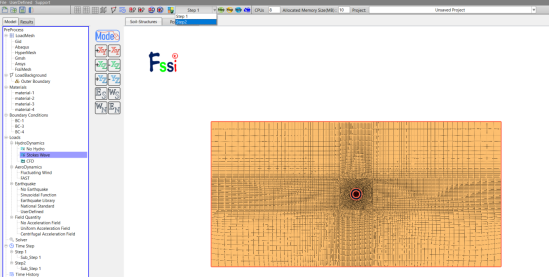
假定土体均匀各向同性,稳态渗流,地下水不可压缩,忽略介质的自重。同时假设材料的渗透系数在各个方向相同,且渗流方向以径向为主,则渗流体积力中浮力部分比例较小,为研究海底隧道开挖后地下水渗流的影响机制,浮力的影响可暂不考虑。模型平面图如图1所示,假定半径b以外形成的稳定渗流场水头与隧道中心点的原始静水压力水头H相等,本文中,取H =b,将b作为模型计算外边界水头。在以上假设前提下,可近似按轴对称平面应变问题计算海底隧道地下水渗流场分布。
模型尺寸为 400 m×60 m,模型的左、右和下边界为不透水边界,上边界和隧洞内边界为定水头边界,给水边界水头H =40m,设衬砌内部水头H1 = 0 模拟全排水情况,隧道内径5m,衬砌厚度0.5m,注浆圈厚度2.5 m,其他参数如下:
表1 实验参数设置
岩性 弹性模量/Pa 泊松比 粘聚力/MPa 摩擦角/(°) 密度/(kg/m3) 渗透系数/(m/s)
围岩 97e6 0.4 0.24 30 1800 1e-6
注浆圈 5e9 0.3 0.8 35 2000 1e-7
衬砌 10e9 0.3 1.5 40 2400 5e-8
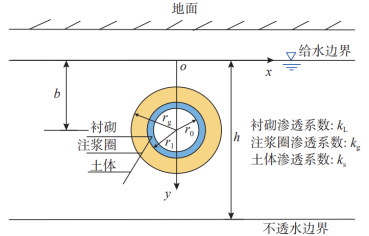
图1 模型草图
1.引言
随着我国水利、交通、地下储油储气洞库的迅速发展,海底隧道的建设正面临高水压问题,导致隧道结构防水困难;同时,海底隧道特殊的“V”形结构[1],使得隧道无法实现自然排水。因此,海底隧道作为一项大体量、高风险工程,涌水问题在隧道设计和建设过程中都备受关注[2]。隧道渗流场孔隙水压分析对隧道的施工安全和使用寿命影响重大。
国内外学者对海底隧道渗流问题进行了大量研究与实践,取得了一系列研究成果。渗流场的理论研究方面,有基于竖井理论的无限地层法[3]、基于复变函数保角变换法的半无限地层渗流场解析解[4]、基于镜像法的有限含水层隧道渗流模型[5]等,采用不同的理论分析了注浆圈和衬砌作用下的单孔隧道线性或非线性渗流问题的解析解,并与实验结果、数值模拟[6-7]进行了对比分析,验证解析解的适用性。随着计算机技术的发展,数值模拟已经成为有效地解决复杂水文地质问题的另一种方法。在目前隧道渗流数值模拟中,有限差分法和有限元法应用较普遍,秦松[8]使用有限差分软件FLAC 3D研究了复杂地质海底隧道渗流场特性和隧道稳定性。LI et a1[9]采用大尺度物理模型实验和数值模拟的方法对涌水过程进行研究,分析了隧道施工过程中涌水机理以及位移场和渗流场的关系,对支护结构设计参数提出建议。熊文威等[10]采用ABAQUS分析确定了高渗透压压下隧道的合理排水设计方案和支护参数,在工程应用中效果良好。FSSICAS(Fluids-Structures-Seabed Interaction- Chinese Academy of Sciences,简称FSSI或FSSICAS)是由武汉岩土力学研究所叶剑红研究员及其团队自主研发,具有自主知识产权,是国际上能够考虑复杂水动力条件、复杂几何边界、土的复杂本构模型的同类软件中较为先进的计算软件之一。FSSICAS软件基于体积平均雷诺数平均纳维尔-斯托克斯方程和Biot动态方程,采用自主研发的耦合算法,将流体动力学和结构物动力响应耦合为一个整体,用以研究波浪冲击下海洋结构物及其海床地基的动力响应。软件支持多种材料本构模型,具有高效的CPU并行计算功能和CPU-GPU联合并行计算能力,十分适用于计算研究近海环境中波浪/地震与近海结构物、海床地基之间的相互作用机理,并定量评价近海结构物在波浪水动力、地震作用下的安全稳定性。此外,FSSICAS软件还适用于传统岩土工程中的流-固耦合问题,如基坑开挖、隧道渗流与变形等。
目前对海底隧道的渗流研究大多集中在单孔或双孔隧道渗流问题,考虑交通流动性、安全性和可靠性等方面的优势,海底隧道以三孔并行的布置方式居多。三孔并行隧道之间渗流场如何互相影响是目前需要解决的问题。基于上述研究进展和软件介绍,本文首先考虑有限含水层圆形单孔隧道工况,将理论解[5]与ABAQUS数值解、FSSI数值解进行对比,分析了含水层厚度和注浆圈参数对孔隙压力的影响,之后基于工程实际建立两主隧道+服务隧道的三孔模型,分析了孔间泄压作用对隧道渗流的影响。
2.FssiCAS模型求解
2.1 Abaqus建模
2.1.1 草图绘制
本案例进行数值计算的是二维模型,先通过Abaqus绘制草图,创建数值计算模型。打开Abaqus后,创建一个新的Standard/Explicit模型,选择Sketch创建草图,如图2所示,本次草图模型命名为tunnel。
图2 Abaqus数值模型边界线草图
2.1.2 创建模型材料并赋参
选择Part创建部件,选择二维平面上的可变形壳模型,导入草图tunnel,创建部件,如图3所示,这里依据实际情况对草图进行平移或其他操作,使坐标对应。之后删除隧道内部分草图,生成完整的土体结构。之后,点击拆分面→来自草图,导入草图tunnel后同样进行移动操作,使得草图和实体重合,点击分区几何,完成分区。
进入材料模块,定义Material-1到Material-4依次为土体、注浆圈、衬砌和被开挖土体,这里不需要输入材料具体参数。之后对材料赋予截面,均为实体均质材料,Section-1到Section-4对应Material-1到Material-4。之后指派截面,按照命名原则指派具体实体区域,指派完成的材料为绿色,如图4。

(a)导入草图
(b)生成土体
(c)分区几何
图3 Abaqus创建并编辑截面
(a)定义材料
(b)定义材料截面
(c)指派材料截面
图4 Abaqus指派截面到模型
2.1.3 划分网格
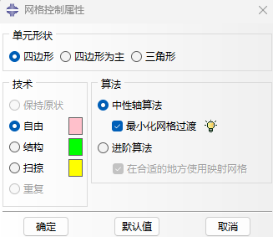
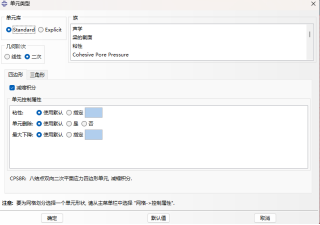
进入网格模块,Abaqus 网格划分主要分为三个步骤,首先考虑合理的网格稀疏性,对实体继续进行面切割,类似图3中的操作。接下来布置种子,考虑FssiCAS软件教育版对计算网格数的限制,适当控制全局网格尺寸为1,对局部区域布置局部种子加密和稀疏,采用单精度算法对远离隧道区域采取1-15大小的过渡。隧道内部采用0.3的网格模拟;其次控制网格属性及类型,为保证精读,部件采用四边形单元计算,采用中性轴算法。接下来对单元类型进行指派,为了计算结果更加的准确,四边形选择高精度的 CPE8R 单元类型,最后生成网格,如图5,6所示。
(a)进一步划分网格区域
(b)设置局部种子
(c)设置网格控制属性
(d)设置单元类型
图5 Abaqus网格单元设置

图6 Abaqus网格生成
2.1.4装配
装配部件,并对部件平移,如图7,确保写出文件中的坐标信息正确。

图7 Abaqus装配部件
2.1.5 输出inp和igs
工作区选择Job创建作业,并写入 input文件。
依次点击文件—导出—草图,后缀选择igs,选择需要的草图,类型选择standard,最后点击确认就可以将igs后缀的背景线文件导出,如图8。
(a)输出inp文件
(b)输出igs文件
图8 Abaqus输出inp和igs文件
2.2 FssiCAS数值计算
2.2.1 导入网格及背景线
打开 FssiCAS 数值计算软件,File→new,新建一个fssi文件,导入 Abaqus的input 文件,全部选择 Solid Element,右侧的Fluid Order 选项与该材料中是否有流体节点有关,包含流体节点的材料选择1,无水层土则设置成0。然后点击Load Background→Outer Boundary导入背景线,导入后明显边界处发黄,如图9。
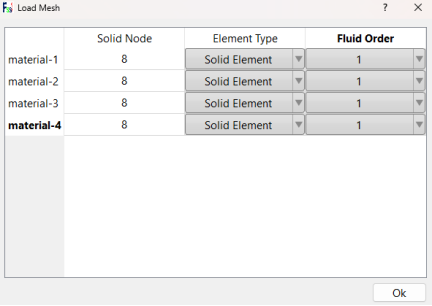
(a)FssiCAS设置材料单元类型
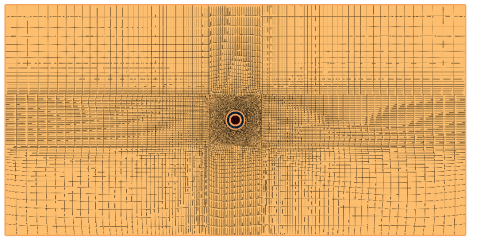
(b)FssiCAS导入边界线
图9 FssiCAS导入ABAQUS文件
2.2.2 设置边界条件
需要将几何模型的边界条件设置为:左右两侧的边界设置为 X 方向位移固定,底部边界设置为X、Y方向位移均固定,侧边界和顶边为固定孔压边界或施加Hydrodynamic边界,隧道开挖边界为全排水边界,孔压为0(如需分步时,在第二步时设置)。点击工具栏中Apply Boundary图标,进入相应的线/面选择模式。点击键盘‘R’键,进行选择,被选中的对象会变亮,通过此操作进行一次设置上述边界,如图10。
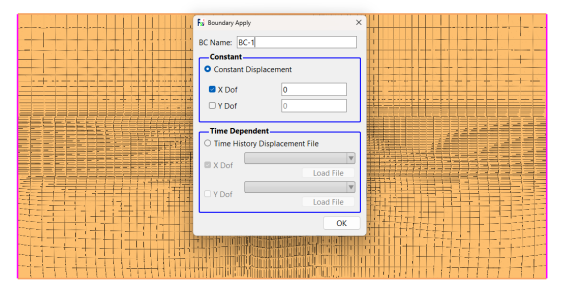
(a)位移边界设置
(b)孔压边界/Hydrodynamic边界设置
图10 FssiCAS边界条件设置
2.2.3 设置材料参数
本模型中共有四种材料,参照表1,其材料参数设置如图所示,在第一个时间步时,所有材料统一设置为土体材料,如图11。
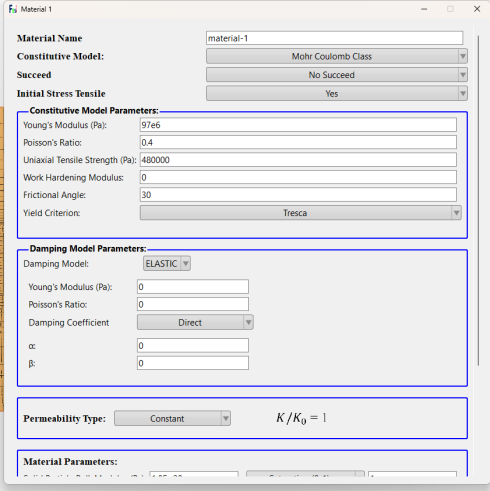
图11 FssiCAS材料参数设置
2.2.4 设置荷载
考虑模型为稳定渗流,依据是否考虑水动力作用和重力作用,选择 No Hydro或者Stokes Wave设置,采用Stokes Wave设置水静力条件时,Wave Period (s)为0.1(较小值),Wave Height (m)和Water Depth (m)设置为0,SWL Position (m) 为Hydrodynamic边界处的水头值。在Y方向进行重力场设置,依据是否有重力设置重力加速度为0或9.806m/s2,如图12。
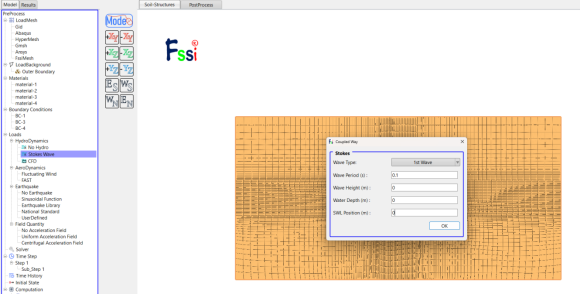
(a)Stokes Wave边界设置
(b)重力边界设置
图12 FssiCAS荷载设置
2.2.5 设置求解过程
对求解器,在前处理界面上 Model 树状菜单栏里的 Solver 中,点击 Solver Type,在弹出的对话框中设置求解器类型,求解器设置为 Static(Static 表示与时间无关的静态,为了获得初始状态最好用 static 求解器),并进行相关属性参数设置,如图 13所示。
时间步设置如下:通过点击Preprocess—Solver—Time Step设置时间步Step1。Simulation Time(s)为计算总时间,设置为1s;Interval for Time Steps(s)为时间步长,设置为0.1 s;Interval for Updating Coordinate(s)为坐标更新时间,设置为2s (大于计算总时间,意为不更新坐标);Interval for Updating Global Stiffness Matrix (s)为刚度矩阵更新时间,设置为2 s (不更新刚度矩阵);Maximum lterations 为每个时间步最大迭代次数,设置为10步;estart File OuputInterval(s)为输出重启文件的时间,设置为 2s (不生成重启文件);Result File Ouput Interval(s)为输出某一时刻所有节点/高斯点上的位移、应力、应变等结果文件的时间间隔,设置为每0.1 s输出一次结果文件,Results Sequence为选择输出节点上的结果;History Output Interval(s)为输出特定的节点或单元上的应力、应变等结果文件的时间间隔,设置为每0.1 s输出一次。剩余三项为时间系数,保持默认值即可。同时进行初始条件的设置。
(a) 求解器设置
(b) 时间步设置
(c) 初始条件设置
图13 FssiCAS求解设置
2.2.6 设置第二个时间步
上述操作默认在设置step1,即地应力平衡,在考虑重力作用时,ABAQUS需要考虑注浆、应力释放、添加衬砌、移除土体等多个分析步,在本算例中做简化,将这些时间步统一为一个时间步step2进行处理:
点击上方绿色step按钮,新建时间步,命名为step2,之后切换时间步到step2中。将material-2,material-3替换为注浆圈、衬砌参数。点击时间步右侧的开挖按钮,点击左侧出现的Excavation and Build,选择material-4为开挖区域。添加边界条件:隧道开挖边界为全排水边界,孔压为0,其他条件默认不变,重复2.2.4设置step2的求解设置,如图14。
(a)新建时间步
(b)切换时间步
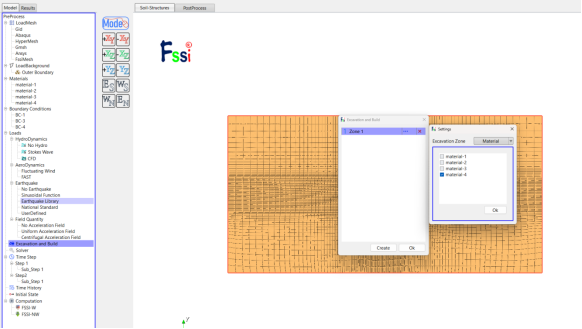
(c)设置开挖部分
图14 FssiCAS第二时间步设置
补充:设置监测点:
对衬砌和注浆实体网格的节点和单元竖直与水平方向布置观测点。先在伸缩区选择输出固体或流体节点,之后在工具栏点击Time History, “R”键选中需要关注的点或单元,右击鼠标,选择输出项,如图15 所示。在节点和单元上可输出的所有时程结果,
(a) 选择节点
(b) 设置输出选项
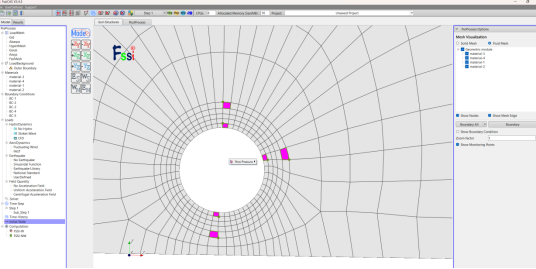
(c) 选择单元
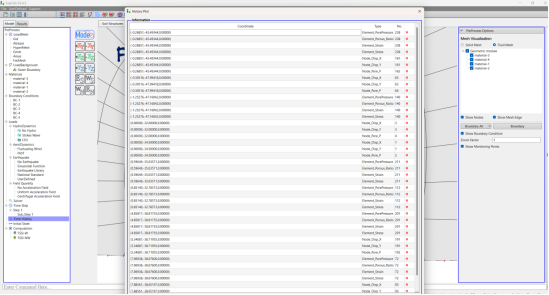
(d) Time History列表
图15 FssiCAS求解设置
2.2.7 求解
前处理界面上 Model 树状菜单栏里 Computaton 中的 FSSI-W,或者在前处理界面正上方的工具栏 2 中的 Write Calculate 功能按钮,点击 All step,保存当前项目,开始计算,计算完成如图16所示。
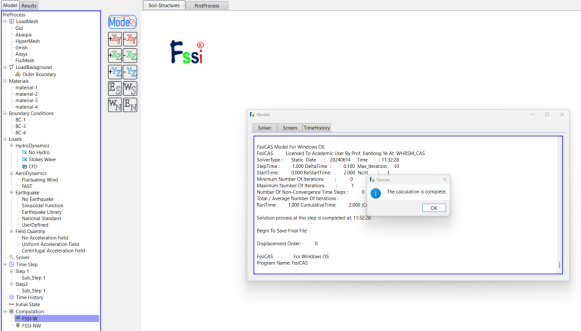
图16 FssiCAS计算结束
2.3 FssiCAS后处理
点击在后处理 Results 树状菜单栏中的 Open Results File,在弹出的窗口中点击 Soil ResultsFiles Director—Load Files,选择需要处理的结果文件夹 Results—Soil_Model—Multiple,进入后处理阶段。
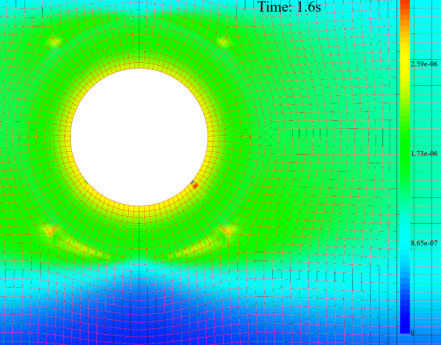
点击 FssiCAS—Postprocess—Distribution—Solid & Structures ,可以选择绘制位移、应力、孔压等计算分布图,如图17。由于FssiCAS无法计算渗流量,本案例主要关注孔压。
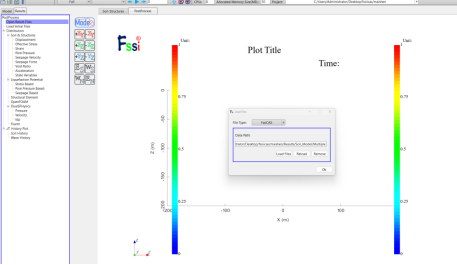
(a) 导入文件
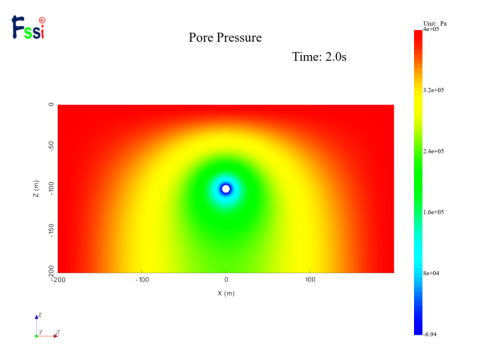
(b) 孔压结果
图17 FssiCAS孔压结果图输出
点击 FssiCAS—Postprocess—History Plot—Soil History ,在伸缩区输入坐标,Plot Type选择Pore Pressure,可以导出关键点的孔压变化图,如图18所示。或者将模型以节点的形式显示,在右侧框中将节点孔隙水压值输出到ExportFiles中,如图19所示。
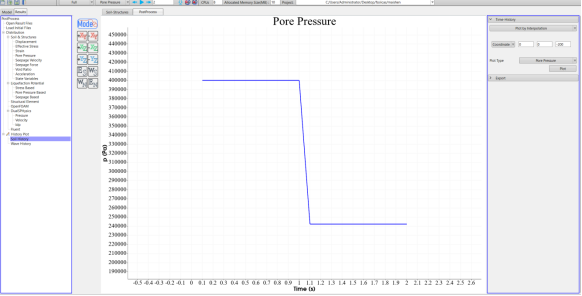
图18 FssiCAS孔压时程图输出
图19 FssiCAS节点值输出
3.与理论解对比
3.1 总水头分布对比
马少坤[5]等基于镜像法推导有限含水层内隧道渗流场解析解如下:
土体区域水头:
(1)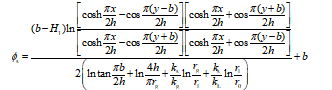
衬砌区域水头:
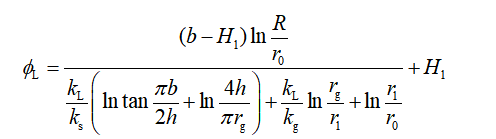
(2)
注浆圈区域水头:
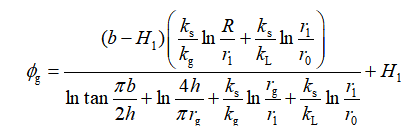
(3)
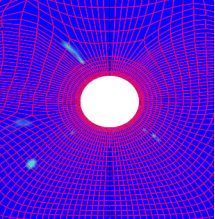
式中的具体变量含义见图1,通过编写MATLAB程序得到理论解的水头等值线,由于Fssi计算软件无法输出孔隙水压等值线,在此将土体的Fssi孔隙水压计算云图与理论解水头等值线对比如图20。在不透水边界上,流线方向水平,Fssi孔隙水压等值线大致垂直于边界,本文Fssi解的计算值与理论解结果基本吻合。
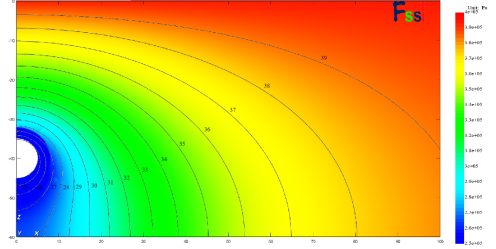
图20 Fssi计算结果与理论解对比(图中黑线为理论解水头等值线)
3.2 特征点水头对比
同时采用Abaqus软件建立二维隧道渗流模型进行计算,为进一步定量分析,分别读取 0°、90°、180°方向上的衬砌、注浆圈特征点的水头计算结果,如表2 所示。
表2 水头不同数值软件解与解析解对比
点号位置 A/A1 B/B1 C/C1
Fssi解/m Abaqus解/m 解析解/m Fssi解/m Abaqus解/m 解析解/m Fssi解/m Abaqus解/m 解析解/m
衬砌外侧 9.01 9.07 9.01 9.59 9.56 9.01 8.30 8.29 9.01
注浆圈外侧 26.70 26.76 26.73 28.49 28.47 26.73 24.51 24.56 26.73
对比数据可看出,Fssi解与Abaqus解十分接近,最大误差不超过1%;隧道底部特征点C/C1处水头的数值解均小于解析解,顶点B/B1处水头则相反。考察解析解推导过程,这是因为对隧道外边界采用了等水头假定,但是当边界条件不可忽视的情况下,在Fssi中(或实际情况下)是不可能满足等水头条件的。因此二者在隧道底部位置的水头差略大,其中Fssi中靠近不透水边界的隧道底部的水头有所削减。总体来说,Fssi解与Abaqus解误差很小,说明Fssi解十分准确。
4.参数分析
参考典型隧道工程 (厦门海底隧道[11]、双碑隧道[12] 等) 及相关解析解进行分析,隧道涌水量、土体中的水头分布主要与隧道埋深d、各介质的渗透系数(ks、kg、kl)、注浆圈参数等有关,与现有的解析解相比,本文解可同时考虑隧道渗流场上、下边界的影响。本节结合该简单算例,讨论有限含水层条件下各参数对解析解的影响。除了变量参数以外,算例参数同表1。
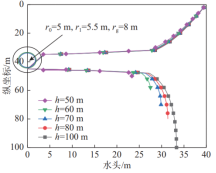
4.1 含水层厚度的影响
其他参数不变,分别取h=50m、60m、80m、120 m、200m,隧道竖向对称轴上的水头沿深度分布情况如图21所示。由图21可知,无论是否考虑重力作用,轴线上点的水头都随着含水层厚度的增大而增大,隧道下方的水头增大得比隧道上方明显。这表明半无限地层假定会显著高估隧道周围的水头值。对于本案例中的浅埋隧道(埋深≤50m),衬砌水头、注浆圈水头计算结果误差均在10%以内,且隧道下方水头均大于隧道上方水头,这表明解析解的隧道外等水头假定有误差;轴线上土体水头差异较大,这表明分析土体含水层厚度对土体的孔隙水压变化的影响时,应考虑重力作用,解析解不完全适用于土体孔隙水压计算。
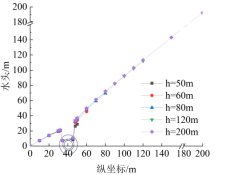
(a)
(b)
图 21 含水层厚度对隧道竖向轴线上水头的影响
(a)考虑重力作用 (b)不考虑重力作用[5]
4.2 注浆圈的影响
在不同含水层厚度条件下,衬砌外水头随着注浆圈抗渗性的变化而改变的趋势一致。如图22所示,随着注浆圈抗渗性的增大,衬砌外水头呈先急剧后趋向缓慢的递减趋势。衬砌外水头随着含水层厚度的增大而略微增大,说明提高注浆圈抗渗性对衬砌外水头的降低作用受不透水边界的影响较小。
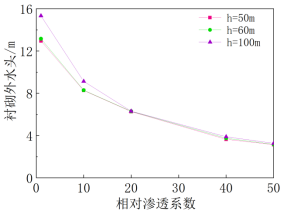
图 22 衬砌外水头和相对渗透系数的关系
4.3 多孔隧道的影响
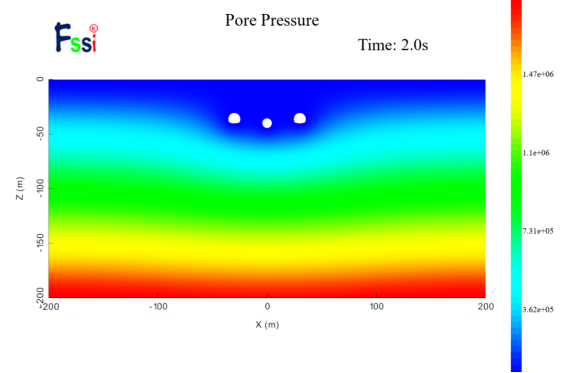
参考厦门海底隧道实际隧道断面和埋深情况[11],建立毛洞模型如图23,主隧道采用钻爆法施工,隧道开挖面积约为162.7m2,服务隧道采用盾构法施工,开挖直径为5m,隧道间距30m,埋深30m,顶部边界施加200 kPa固定孔隙水压力。计算结果如图23,隧道开挖后,在隧道周边一定范围内形成“压降漏斗”,隧道之间互为“泄压孔”,降低了隧道间的孔隙水压力,同时也再次验证了FSSI软件的准确性。在隧道竖直与水平轴线方向设置4条不同的测线,分析其孔隙水压力变化,如图24所示。
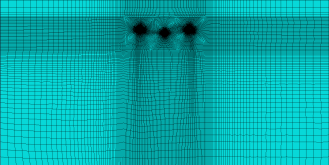
(a) 模型截图
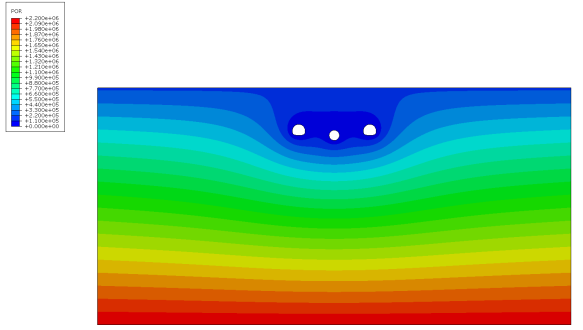
(b) ABAQUS解
(c) FSSI解
图 23 数值解对比
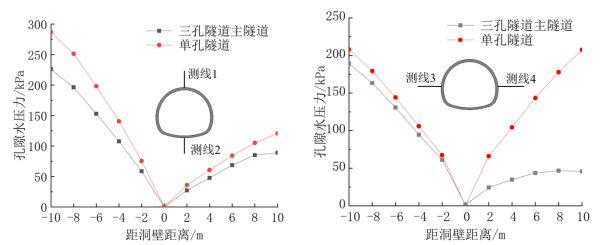
图24 覆岩厚度30 m时不同测线孔隙水压力分布规律
与单孔隧道相比,三孔隧道的孔隙水压力整体低于单孔,孔隙水压力的增长速率也比较低。竖直方向上,隧道上方受到的泄压影响较弱,水平方向则由基本对称变为在测线4方向显著降低,随着距隧道壁距离的增加,孔隙水压力先是上升,然后稳定并有下降趋势,这是因为测线4方向与邻近隧道距离较近,由此也说明距离隧道越近泄压作用越明显。
5.讨论
5.1 边界条件的影响
在本案例的计算过程中,涉及到流体边界条件怎么施加的问题,结合论文[6,10-12]和师兄答疑,施加水力条件的方法,在FSSI中,有考虑重力时采用固定三边(两侧和上边界)孔压+重力场或三边施加Stokes Wave+重力场都可以实现考虑重力的水力条件施加,本文对原始案例施加上述两种条件,孔压200kPa或SWL Position (m) 为20m,重力场统一为-10m/s2,结果如图25,Stokes Wave+重力场边界下结果略低于孔压+重力场,但影响几乎可以忽略,因此,两种方法都可以用于施加考虑重力作用时的静水压。
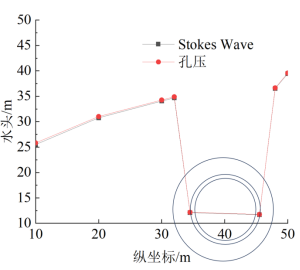
图25 不同施加水力边界的影响
5.2 心得体会
在模拟计算过程中,FSSI给我的最大感受就是计算速度相较ABAQUS快,操作简单,对于本算例来说,孔压分布计算结果很准确。如果能在后期云图处理过程中加入等值线和等值线数值的显示功能,这样显示结果更直观。另外就是希望能加入计算涌水量的功能,像FLAC 3D内置Fish函数一样,取单位长度隧道外围节点的不平衡流量之和,以此作为隧道的涌水量。
结合老师和师兄们答疑课上的答疑,FSSI似乎对网格质量的要求比ABAQUS的高一些,在如下的一个模型进行计算时,如图26,先用ABAQUS自带的网格质量检测功能进行检测,报警告的网格部分在FSSI计算时都会有突变。接下来不断的优化网格划分方法,如图27,优化后报警告的四个网格均在开挖土体部分,第二个时间步会被挖掉,不过在采用FSSI计算渗流速度时,在未报错或警告的部分出现了部分节点处的数值突变,无论采用静态还是动态求解器,多少个时间步都会有类似的情况。这些部分几乎都是是在注浆圈和土体交界面的过度网格的地方以及警告网格的附近。如何能够更合理的划分网格,处理好不同图形之间网格的更优划分是我觉得日后自己需要重点学习和改进的地方。
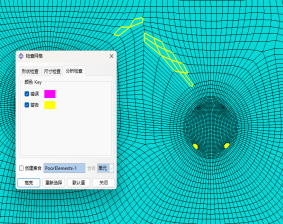
(a)网格质量检测结果
(b)FSSI计算奇异点
图26 初始网格划分
(a)网格质量检测结果
(b)FSSI计算奇异点
图27 改进网格划分方法
6.结论
本文主要对不同含水层厚度隧道渗流场的理论解与数值解结果及其影响因素进行对比,主要结论如下:
(1)理论解适用于求解隧道衬砌和注浆圈外水平方向的水头,在数值方向上由于等水头假定的局限性,理论解与数值解存在误差,但Fssi与Abaqus数值解误差很小,这说明FSSI数值模拟计算效果的准确性。
(2)注浆圈的存在以及抗渗性的不断增强会降低含水层厚度的影响,随着注 浆圈相对渗透系数的增加, 隧道衬砌外水压呈非线性降低趋势,围岩与注浆圈渗透系数比值小于40时,注浆圈渗透系数对涌水量和衬砌外水压力的敏感性显著;当比值大于40后,影响较弱。综合来看,两者比例取值 20-40 左右较为恰当,与论文推荐值[5]接近。
(3)孔间的泄压作用整体降低了孔压,主隧道渗流速度呈现出明显的非对称性,靠近服务隧道的一侧降低效果更加明显,一定程度上可减小渗流破坏。
参考文献(References):
[1]HARR M E. Groundwater and Seepage [J]. Soil Science,1963, 95(4): 289.
[2]《中国公路学报》编辑部.中国交通隧道工程学术研究综述-2022[J].中国公路学报,2022,35(4):1-40.
Editorial Department of China Highway Journal. A Comprehensive Review of Academic Research on Chinese Transportation Tunnel Engineering - 2022 [J]. China Highway Journal, 2022, 35(4): 1-40.
[3]王秀英,王梦恕,张弥.山岭隧道堵水限排衬砌外水压力研究[J].岩土工程学报,2005(1):125-127.
WANG Xiuying,WANG Mengshu,ZHANG Mi.Research on regulating water pressure acting on mountain tunnels by blocking ground water and limiting discharge[J].Chinese Journal of Geotechnical Engineering,2005(1):125-127.(in Chinese).
[4]HUANGFU M, WANG M S, TAN Z S, et al. Analytical solutions for steady seepage into an underwater circular tunnel [J]. Tunnelling and Underground Space Technology, 2010, 25: 391-396.
[5]马少坤,陈彩洁,段智博,刘莹. 基于镜像法的有限含水层内隧道渗流场解析解及其验证[J]. 工程力学, 2023, 40(5): 172-181.
Ma Shaokun, Chen Caijie, Duan Zibo, Liu Ying. Analytical Solution of Seepage Field in Finite Aquifer for Tunnel Based on Image Method and Its Validation [J]. Engineering Mechanics, 2023, 40(5): 172-181.
[6]王育奎,徐帮树,李术才,等.海底隧道涌水量模型试验研究[J].岩土工程学报,2011,33(9):1477-1482.
Wang Yu-Kui, Xu Bang-Shu, Li Shu-Cai, et al. Experimental Study on Water Inrush Model of Submarine Tunnels [J]. Chinese Journal of Geotechnical Engineering, 2011, 33(9): 1477-1482.
[7]陈俊儒,王星华.海底隧道涌水量的预测及其应用研究[J].现代隧道技术,2008(5):18-21.
Chen Jun-Ru, Wang Xing-Hua. Prediction and Application Study of Water Inrush in Submarine Tunnels [J]. Modern Tunnelling Technology, 2008(5): 18-21.
[8]秦松.复杂地质海底隧道不同防排水体系下渗流场及变形特征研究[J].公路交通科技,2023,40(5):138-145.
Qin Song. Study on Seepage Field and Deformation Characteristics of Submarine Tunnels with Complex Geological Conditions under Different Drainage Systems [J]. Journal of Highway and Transportation Research and Development, 2023, 40(5): 138-145.
[9]LI Shucai,LIU Hongliang,LI Liping,et al.Large scale three-dimensional seepage analysis model test and numerical simulation research on unders ea tunnel[J].Applied Ocean Research,2016,59:510-520.
[10]熊文威,汪波,蒙伟,等.高水压水下隧道合理涌水量限排设计研究[J].铁道标准设计,2022,66(12):104-110.
Xiong Wen-Wei, Wang Bo, Meng Wei, et al. Research on the Rational Design of Water Inrush Limit Discharge for High-Pressure Underwater Tunnels [J]. Railway Standard Design, 2022, 66(12): 104-110.
[11]闫科宇,李善伟,李航达,等. 考虑洞间影响的三孔并行海底隧道渗流问题分析[J]. 石家庄铁道大学学报(自然科学版), 2024, 37(01): 39-44.
Yan Keyu, Li Shanwei, Li Hangda, et al. Analysis of Seepage Flow in Parallel Underwater Tunnels with Three Holes Considering the Influence of Holes on Each Other [J]. Journal of Shijiazhuang Tiedao University (Natural Science Edition), 2024, 37(01): 39-44.
[12]惠云杰. 隧道尺度对衬砌背后水压力的影响机理研究[J]. 石家庄铁路职业技术学院学报, 2023, 22(04): 1-5.
Hui Yunjie. Study on the Mechanism of Tunnel Scale Affecting Water Pressure Behind Lining [J]. Journal of Shijiazhuang Railway Vocational and Technical College, 2023, 22(04): 1-5.
附:Matlab解析解的编写
1.衬砌/注浆圈水头求解:
ks = 1e-6; % 土体渗透系数,单位:m/s
kg = 1e-7; % 注浆圈渗透系数,单位:m/s
kl = 5e-8; % 衬砌渗透系数,单位:m/s
b = 11; % 隧道中心到给水边界的距离,单位:m
H1 = 0; % 隧道内边界处的水头,单位:m
r0 = 5; % 隧道内径,单位:m
r1 = 5.5; % 衬砌外径,单位:m
rg = 8; % 注浆圈外径,单位:m
h = 100; % 含水层厚度,单位:m
R1 = linspace(r0, r1, 100);
R2 = linspace(r1, rg, 100);
% 计算衬砌区域内的水头
C1 = (kl/kg)(log(rg / r1)) + log(r1 / r0);
C2 = (kl/ks)(log(tan(pi * b / (2 * h))) + log(4 * h / (pi * rg))) ;
phiL = zeros(size(R1));
for i = 1:length(R1)
phiL(i) =(b-H1) * log(R1(i) / r0)/(C1+C2);
end
% 计算注浆区域内的水头
C3 =(ks/kg)(log(rg / r1)) +(ks/kl)(log(r1 / r0));
C4 = (log(tan(pi * b / (2 * h))) + log(4 * h / (pi * rg))) ;
phiz = zeros(size(R2));
for i = 1:length(R2)
phiz(i) =(b-H1) * ((ks/kg)log(R2(i) / r1)+(ks/kl)(log(r1/ r0)))/(C3+C4);
end
% 合并函数
R = [R1, R2];
phi = [phiL10009.81, phiz10009.81];
plot(R, phi);
xlabel('注浆圈或衬砌内一点到隧道中心得距离 R (m)');
ylabel('孔隙水压力 (Pa)');
title('孔隙水压力分布');
grid on;
hold on;
plot([r1, r1], ylim, 'k--');
text(r1, mean(ylim), 'r_1', 'HorizontalAlignment', 'right', 'VerticalAlignment', 'middle');
hold off;
2.土体水头求解:
b = 40; % 给水边界到隧道中心的距离,单位米
H1 = 0; % 隧道内边界处的水头,单位米
h = 60; % 含水层的厚度,单位米
rg = 8; % 注浆圈外径
r1 = 5.5; % 衬砌外径
r0 = 5; % 隧道内径
kg = 1e-7; % 注浆圈的渗透系数
ks = 1e-6; % 土体的渗透系数
kl = 5e-8; % 衬砌的渗透系数
x_range = 0:1:100;
y_range = 0:1:h;
[X, Y] = meshgrid(x_range, y_range);
phi_s = zeros(size(X, 1), size(X, 2));
% 计算每个点的总水头值
for i = 1:size(X, 1)
for j = 1:size(X, 2)
arg1 = cosh(piX(i,j)/(2h)) - cos(pi(Y(i,j) - b)/(2h));
arg2 = cosh(piX(i,j)/(2h)) + cos(pi(Y(i,j) + b)/(2h));
arg3 = cosh(piX(i,j)/(2h)) - cos(pi(Y(i,j) + b)/(2h));
arg4 = cosh(piX(i,j)/(2h)) + cos(pi(Y(i,j) - b)/(2h));
epsilon = 1e-6;
phi_s(i, j) = (b - H1)/2 * (log((arg1arg2)/(arg3arg4)+ epsilon ) /(log(epsilon+tan(pib/(2h)))+log(epsilon+4h/(pirg))+(ks/kg)log(epsilon+rg/r1)+(ks/kl)log(epsilon+r1/r0)))+ b;
end
end
figure;
levels = 25:1:40;
[C, h] = contour(X, -Y, phi_s, levels, 'k');