引言
本文将基于FSSICAS有限元软件进行L型抗滑桩加固土坡的数值模拟研究,并根据已有的L型抗滑桩加固土坡的离心模型试验作为数值模拟的模型及相关参数的选择依据,并将数值模拟结果与离心机模型试验进行验证,并以此为基础,研究L型抗滑桩与I型抗滑桩及非支护原始边坡的位移对比,分析L型抗滑桩的支护效果。最后,利用FSSICAS软件中对加固边坡施加周期恒定规则正弦地震波及非规则的实际地震波,研究地震荷载下L型抗滑桩的动力稳定性。
1.1 研究背景
滑坡灾害因其破坏性大、影响范围广是岩土工程中最严重的灾害之一,对滑坡进行加固措施十分有必要[1]。目前对于滑坡灾害的治理方法有很多种,例如通过削坡、底部填土方法,将边坡重心下移,提高边坡的稳定性,还有通过使用抗滑桩进行边坡的加固,传统等截面抗滑桩自身稳定性较差,在土体松软条件下所受锚固力较低,易失稳倒塌[2]。 针对这一问题,提出了一种新型L型抗滑桩,在抗滑桩底端采用螺栓连接一横段,利用土压力提高其稳定性。
L型抗滑桩由一段竖直桩和一段水平桩连接形成,其水平段可视为一种桩靴。 桩靴可增大桩与地基的接触面积,减少桩腿插入基础的深度,提高插桩和拔桩的安全性[3]。
1.2 离心模型试验
·土体的强度和刚度是由有效应力决定的,常规的 1g 缩尺模型试验无法反应 土层原位应力状态,因此无法准确预测真实土与结构相互作用。利用离心模型试验可以在小模型上模拟现场原型岩土工程条件,离心模型试验通过高速旋转产生的离心力对一个1/N 于 原型尺寸的物理模型施加 N 倍的地球重力加速度 g(即 Ng),从而将模型土体应 力水平还原到原型土体,反映出相同的力学行为,如图 1 示意所示。
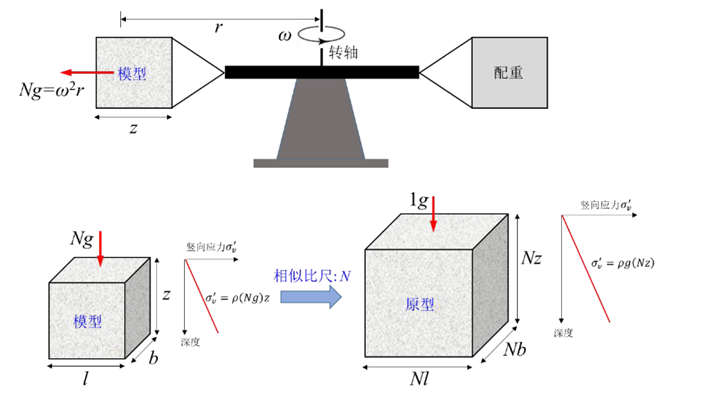
图1 土工离心机工作原理[4]
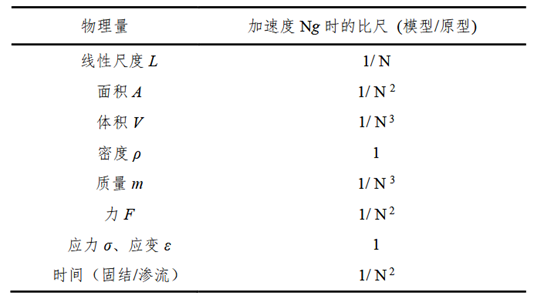
表1 土工离心机试验相关物理量的相似比尺[4]
1.3 L型抗滑桩加固土坡的离心模型试验·
彭秀华[5]等利用离心模型试验方法进行L型抗滑桩加固土坡特性研究。试验中将土坡模型放置在长500mm、宽200mm、高360mm 的模型箱中。图2为L型抗滑桩加固土坡的模型试验示意图及试验模型的照片。试验用黏性土的干密度为1.55g·cm-3,初始含水量为18%。 通过固结排水三轴试验确定饱和黏性土的内摩擦角为30°,黏聚强度为27kPa。
试验中对土坡模型逐级加载,每次增加5g。 每级加载后观测土坡位移变化,确定土坡基本保持平稳运行后(约12min后)再施加下一级荷载,直至加载50g。
2 基于FssiCAS数值模拟
2.1 数值模型与参数
采用由叶剑红研究员团队所研发的有限元软件FssiCAS进行L型桩加固土坡变形特性的二维数值模拟,图3为ABAQUS中建模模型及网格划分图。
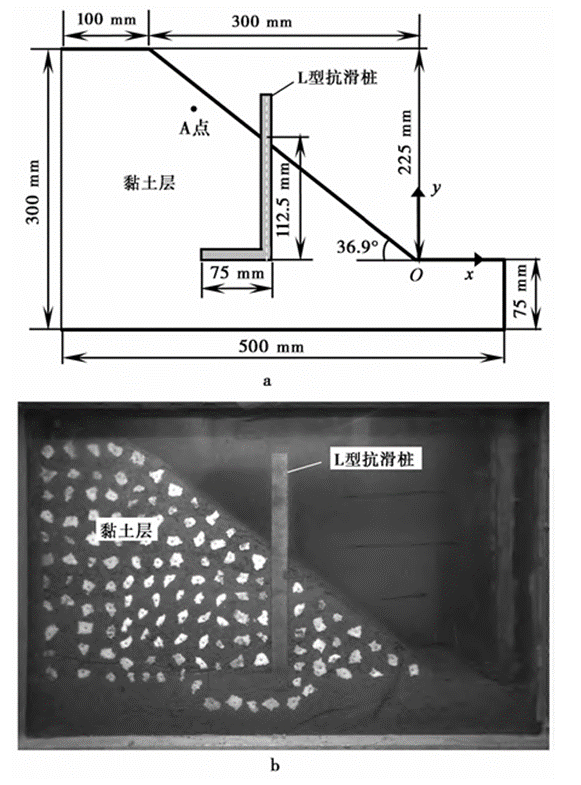
图2 L型抗滑桩加固土坡模型[5]
(a)试验模型结构图; (b)试验模型照片
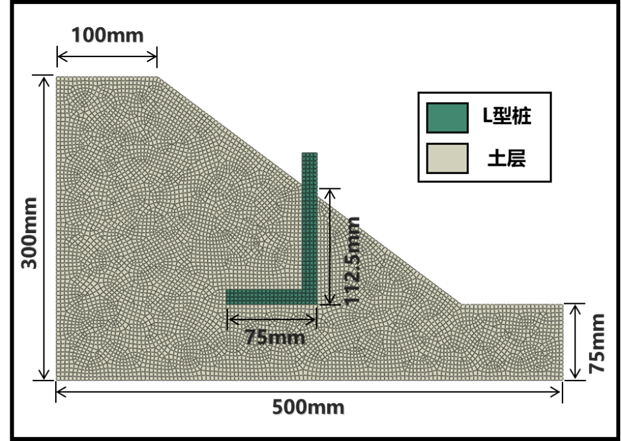
图3 L型抗滑桩加固土坡数值模型及网格划分
表2 材料的模型参数

2.1.1 导入网格
点击FssiCAS—Preprocess—Load Mesh,在弹出的文件选择对话框中选择 Abaqus 输出的*.inp 网格文件,双击或点击打开按钮。在弹出对话框设置中流体节点阶次设置为0,点击OK按钮确认
选择。确认后便可以得到加载完成的模型网格,如图4所示。
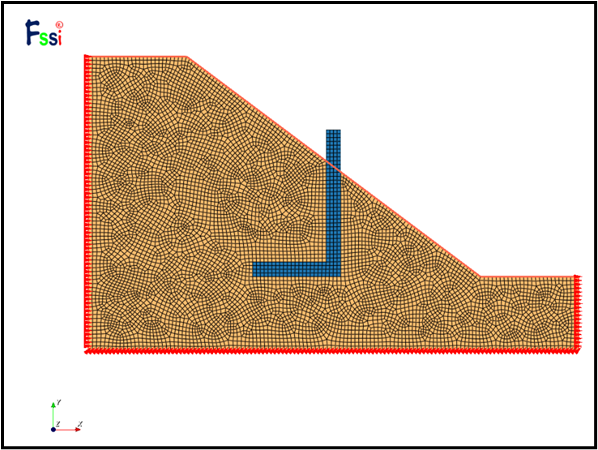
图4 L型抗滑桩加固土坡数值模型(FssiCAS)
2.1.2 添加边界条件
本数值模型需要对模型底面(y=0m)处设置x,y方向的位移约束,对模型侧边进行x方向的位移约束。操作方法为:依次点击 及 按钮,通过键盘中的R键可进行边界线的选择,选择后被选中的边界线将变成粉色如图5所示,右键后左键依次点击Displacement-Apply可出现图5右侧界面,勾选X Dof即施加x方向的位移约束,y方向的位移约束施加模式相同。
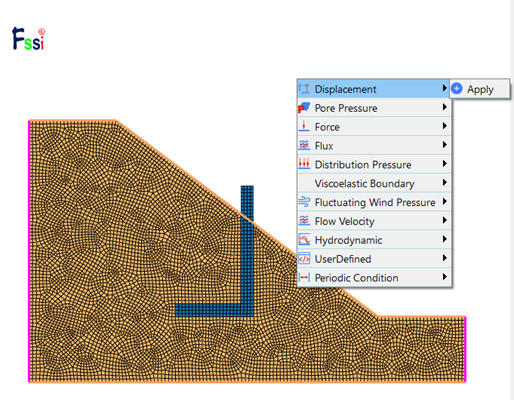
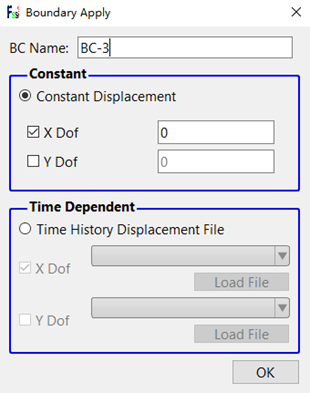
图5 边界条件施加示意图
2.1.3 设置材料参数
点击软件左侧工作区Materials栏下方的材料名称,本文的两种材料参数设置如图6所示,soil材料为边坡土体,pile材料为L型桩,两种材料均使用Mohr Coulomb材料下的Drucker-Prager屈服准则,需要输入材料的杨氏模量、泊松比、黏聚力以及内摩擦角。
2.1.4 设置重力加速度
由于本数值模拟要模拟离心机模型试验,因此重力加速度也要与离心模型实验保持一致,图7为模拟离心机50g条件下的重力加速度设置为-490.3m·s-2。
2.1.5 设置求解器类型
点击FssiCAS—Preprocess—Solver,在弹出对话框中设置求解器类型。在求解器设置时,因为不涉及到动力响应,因此将求解器的类型设置为Static,如图8所示。
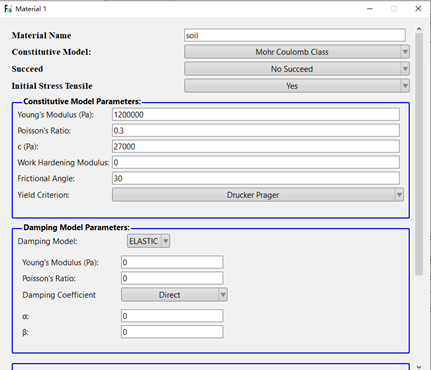
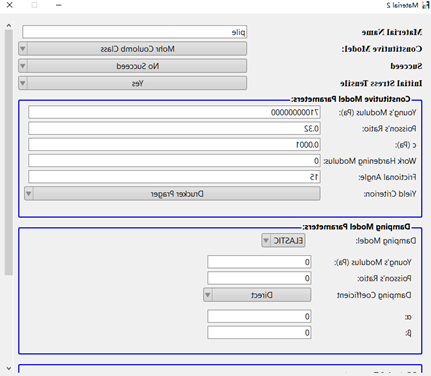
图6 材料参数设置
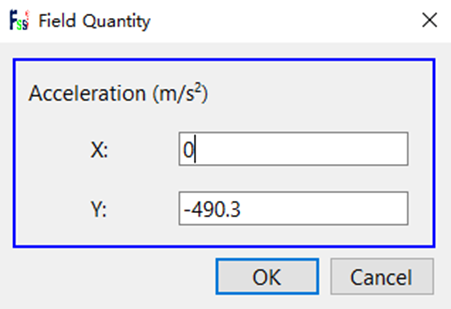
图7 重力加速度设置(50g条件下)
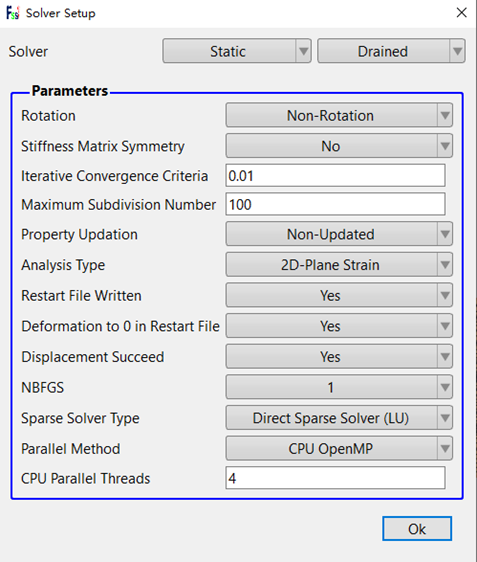
图8 设置求解器类型
2.1.6 设置时间步及初始条件
点击FssiCAS—Preprocess—Solver—Time Step。计算总时长选择为20s,时间步长及数据输出均为0.5s,不更新坐标及刚度矩阵。完成设置后点击Create即可创建时间步。点击FssiCAS—Preprocess—Initial State,设置初始条件,点击ok,完成初始状态设置如图9所示。
完成设置后点击FssiCAS—Preprocess—Computation—FSSI-W,在弹出的对话框中选择All Step 进行计算,图10所示内容为计算完成。
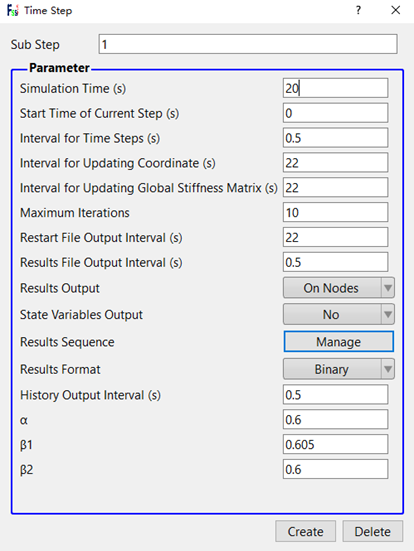
图8 时间步设置
图9 初始条件设置
图10 计算完成
2.2 FssiCAS 图形界面操作——后处理
点击FssiCAS—Results—Postprocess—Open Results File,选择需要处理的结果文件夹,即可导入结果文件夹。点击FssiCAS—Results—Postprocess—Distribution—Soil&Structures—Displacement,在界面上方工具栏选择Displacement X,输入想要查看的时间步点击回车。如果需要其他类型的数据分布图或选择显示数据的方向,可以通过左侧以及上方的选项栏进行选择。右侧的弹出选项栏也可以对分布图的坐标、显示范围、标尺、变形情况等进行设置调整。
2.2.1 数值模拟结果与离心模型试验加载模式对比
首先,由于离心模型试验中的加载流程为对土坡模型逐级加载,每次增加5g。 每级加载后观测土坡位移变化,确定土坡基本保持平稳运行后再施加下一级荷载,直至加载50g。在数值模拟中,为了简化计算流程及保证收敛性,直接将重力加速度增加至50g,为了验证两种方法的误差,先进行对比数值模拟试验:首先将重力加速度直接设置为10g,其结果云图如图11,图12所示;其次使用先将重力加速度由1g提升至5g后再提升至10g的加载模式进行数值模拟,其结果云图如图13,图14所示。根据图11,13以及图12,14的对比,可以看出两种不同的加载方式其水平位移及竖向位移的分布基本相同,因此可以认为,直接加载至50g以及逐级加载至50g在数值模拟中的效果基本一致,因此使用直接加载至50g其结果仍具有可信度。
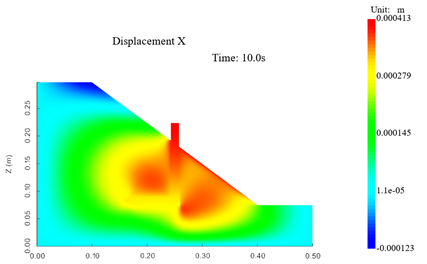
图11 水平位移分布云图(10g)
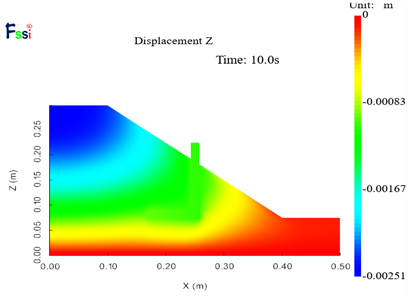
图12 数值位移分布云图(10g)
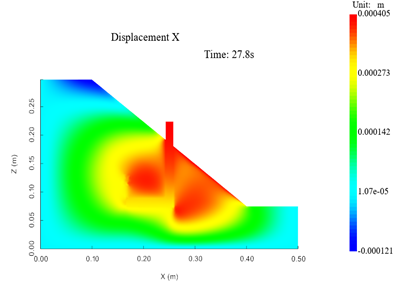
图13 水平位移分布云图(10g)
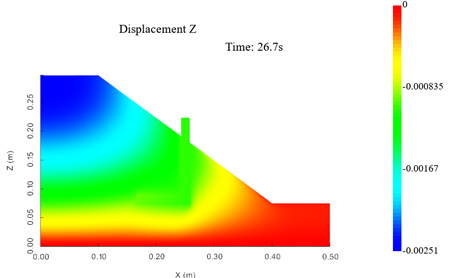
图14 数值位移分布云图(10g)
2.2.2 数值模拟结果与离心模型试验结果对比验证
图15为重力加速度增大过程中典型点A(位置见图图3)的位移时程。 可以看出,试验测量与数值模拟得出的位移变化趋势基本相同,竖向位移随着离心加速度增加基本呈线性增加的趋势。在50g时,数值模拟结果及离心模型实验结果竖向位移分别为17.8mm及17.9mm,水平位移分别为0.685mm及0.68mm,结果接近,初步验证数值模拟的准确性。图16为不同加速度下的水平位移及竖向位移分布云图。
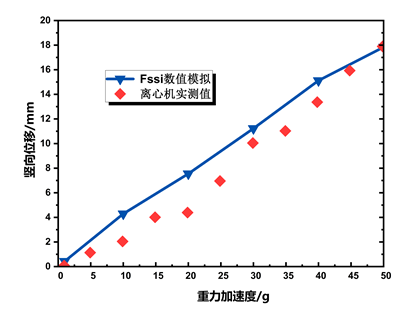
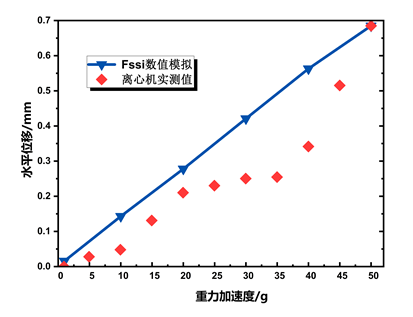
图15离心加速度增加时土坡A点(位置见图3)位移时程)
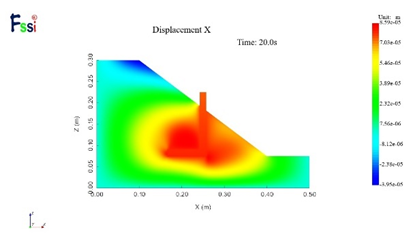
(1)1g下水平位移
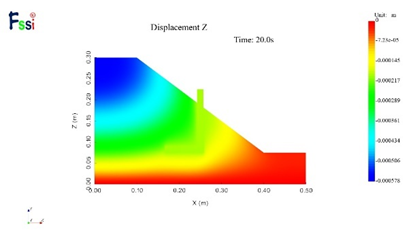
(2)1g下竖向位移
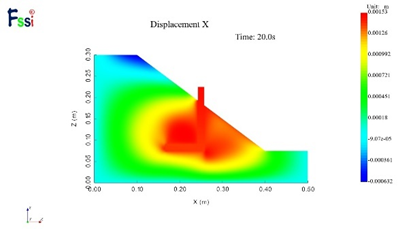
(3)20g下水平位移
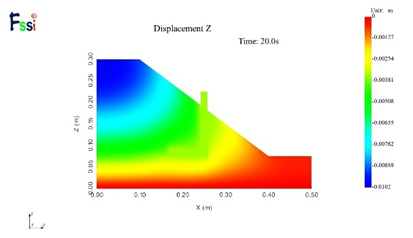
(4)20g下竖向位移
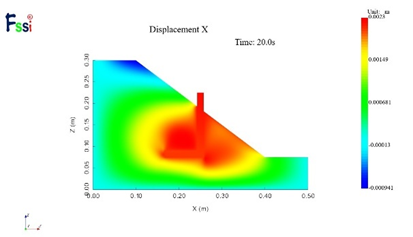
(5)30g下水平位移
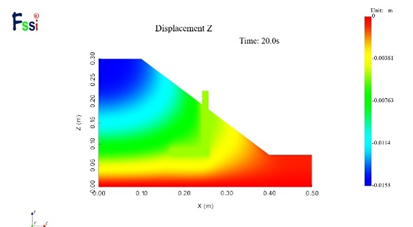
(6)30g下竖向位移
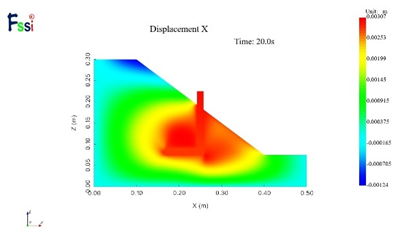
(7)40g下水平位移
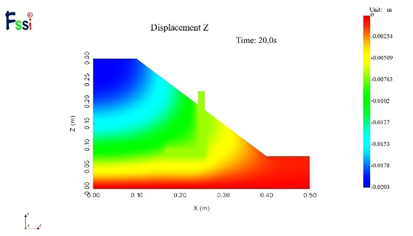
(8)40g下竖向位移
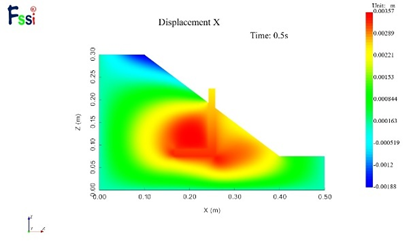
(9)50g下水平位移
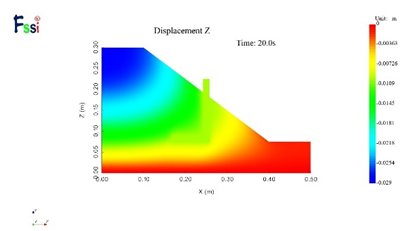
(10)50g下竖向位移
图16 不同加速度下的水平位移及竖向位移分布云图
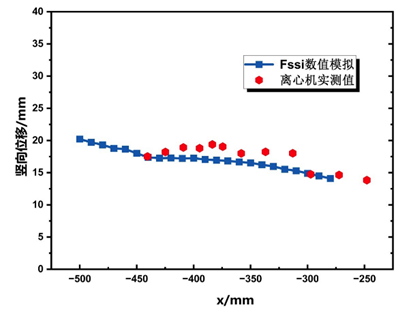
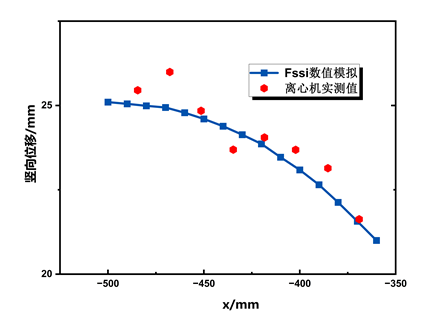
图17 50g时土坡的竖向位移分布对比
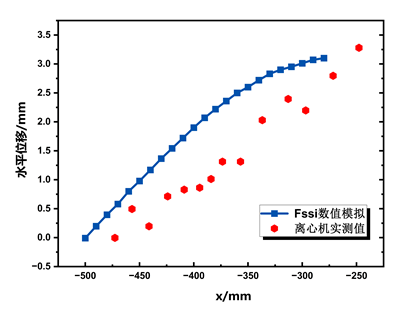
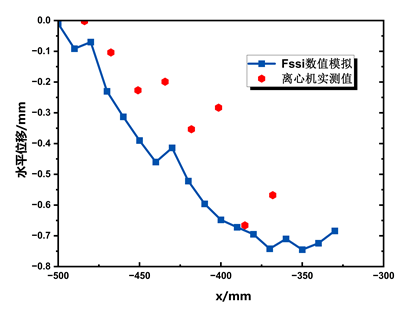
图18 50g时土坡的水平位移分布对比
图17,18为50g时不同高程土坡水平与竖向位移的水平分布。土坡的上部点(y=217.4mm)处水平位移为负值,指向坡内,土坡中部点(y=123.4mm)处土坡的水平位移为正值,以指向坡表为主,其数值在坡表处达到最大值。竖直位移体现出沿着坡面方向位移减小的趋势。通过将FssiCAS数值模拟结果与离心机实测值相比较,可以发现竖向位移结果较为一致,误差不超过5%,水平位移趋势基本一致,数值误差基本在15%以内,部分误差偏大,基本可验证数值模拟的准确程度。
图19为离心模型实验与数值模拟的土坡位移矢量图,通过位移矢量图可以看出离心模型实验的结果与数值模拟结果十分接近,在靠近抗滑桩附近会产生向右侧的土体相对移动,说明其二者的变形模式基本一致,进一步验证了数值模拟结果的合理性。
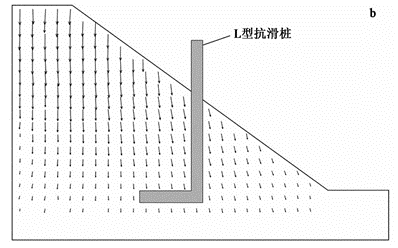
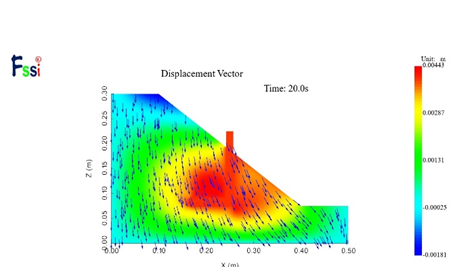
图19 土坡的位移矢量图对比
2.2.3 L型抗滑桩加固效果对比
将L型抗滑桩与I型抗滑桩以及未经加固处理的原始边坡进行数值模拟结果对比,由于边坡稳定性评价重点关心其水平方向的位移变化,因此仅对比其水平位移云图如图20,21,22所示,通过对比三种工况下的水平位移云图,可以直观地看出未支护的边坡水平位移最大,使用L型支护的边坡水平位移最小,三种工况的最大水平位移分别为5.28mm, 5.08mm, 3.57mm。由此可见使用I型支护可以一定程度上减小边坡水平位移,使用L型支护可以更大程度的减少边坡的水平位移。
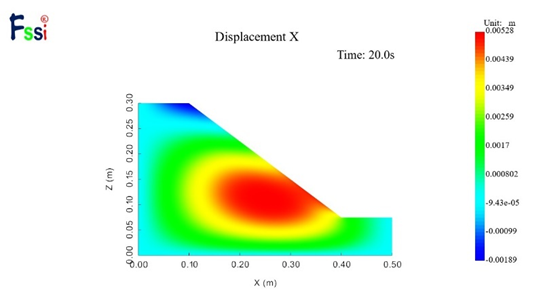
图20 未加固处理的原始边坡水平位移云图
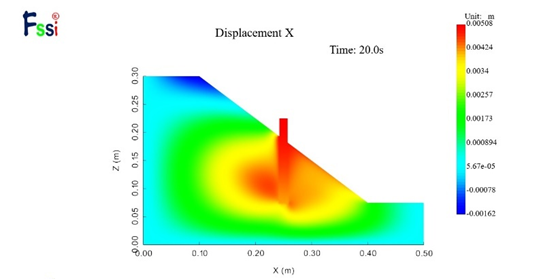
图21 I型抗滑桩的边坡水平位移云图
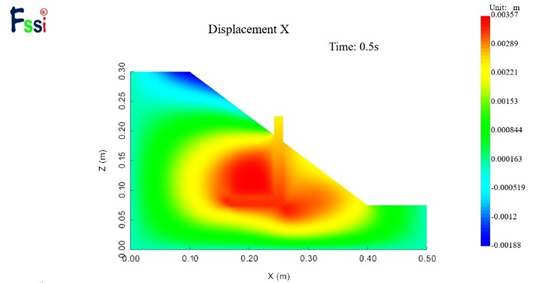
图22 L型抗滑桩的边坡水平位移云图
为了更直观地看出不同支护措施的支护效果,选择(y=217.4mm)时的水平位移沿着x轴方向分布曲线如图23所示。图中显示使用L型抗滑桩支护措施效果最好,水平位移最小,位移最大处为0,8mm,使用I型抗滑桩支护效果小一些,位移最大处为1.4mm,未加固边坡水平位移最大值为1.9mm。两种加固措施与未加固水平位移相比,水平位移分别减少了0.5mm,及1.1mm。说明了L型支护措施可以很大程度上提高边坡的稳定性。
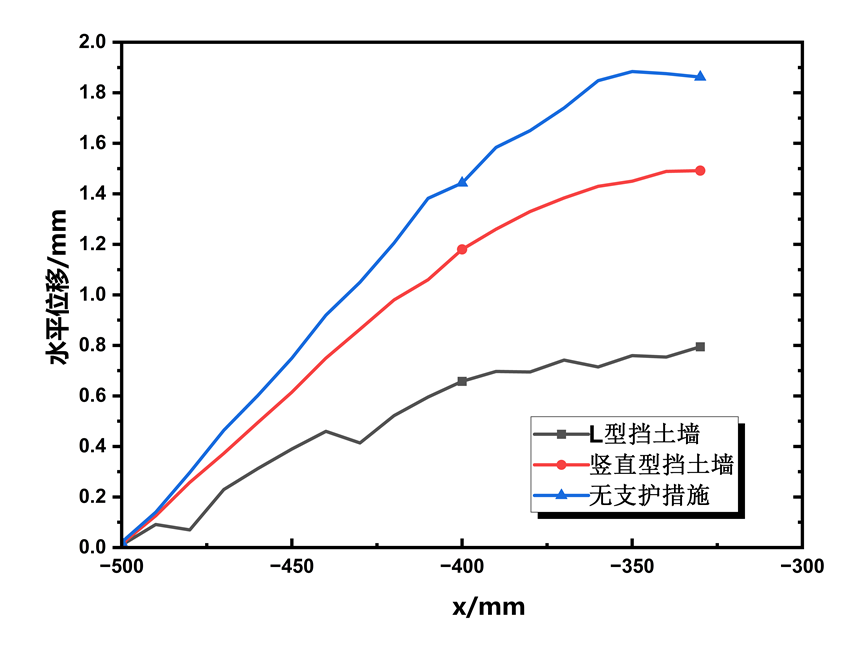
图23不同支护措施的水平位移分布曲线
2.3 地震波作用下的L型及I型抗滑桩边坡稳定性分析
FssiCAS的地震波输入功能十分强大,可以输入正弦地震波、常见的实际地震波以及可以进行用户自定义的地震波输入。本文为了研究地震波作用下的L型及I型抗滑桩边坡稳定性,首先进行正弦周期性的地震波输入,研究不同支护措施下的动力响应。并以此为基础输入用户自定义地震波,进行实际地震波作用下的边坡支护动力稳定性分析。
2.3.1 正弦地震波作用下L型及I型抗滑桩边坡稳定性分析
使用FssiCAS自带的正弦地震模块进行地震波的输入如图24所示。并将求解器类型更改为Dynamic,时间设置为3.5s,左右边界设置为吸收波边界,其余条件均不变。
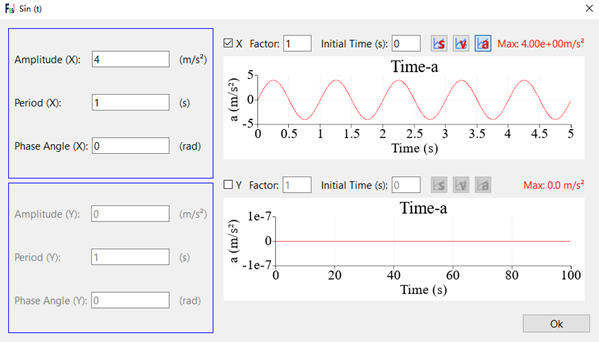
图24 正弦地震波输入曲线
图25为正弦地震波作用下两种支护方式的最大水平动位移云图分布,左侧为I型支护作用下的位移云图,根据图中可以看出L型支护下最大水平动位移为6.17mm,I型支护最大水平动位移为10.9mm,L型支护的最大水平动位移为I型支护的60%,因此在正弦周期性地震波作用下,L型支护的动力边坡稳定性更强,这是由于L型抗滑桩底部与土层的接触面积更大,其抗倾覆的能力较I型抗滑桩更强。
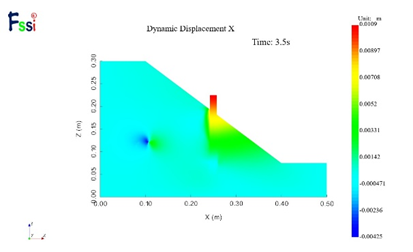
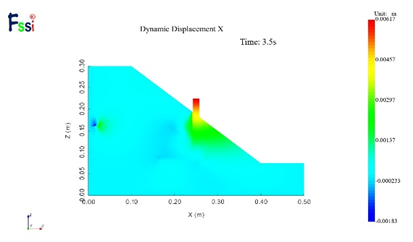
图25正弦地震波作用下水平动位移分布云图
2.3.2 Northbrige地震波作用下L型及I型抗滑桩边坡稳定性分析
为了探究在实际地震中不同支护方式的边坡稳定性评价,本文选用1994年洛杉矶地区发生的北岭大地震(Northridge earthquake)所记录的地震波数据作为输入地震波文件,图26为该地震波的曲线形式。图27左侧为I型支护作用下的位移云图,根据图中可以看出L型支护下最大水平动位移为6.27mm,I型支护最大水平动位移为8.03mm,L型支护的最大水平动位移为I型支护的78%,因此在实际地震波作用下,L型支护的动力边坡稳定性更强,与上文正弦波验证结果相同。
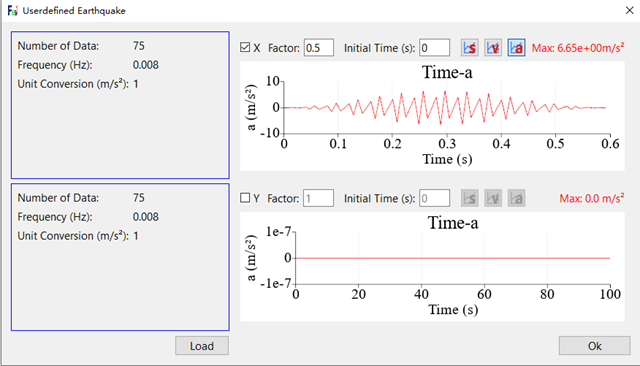
图26 Northbrige地震波输入曲线
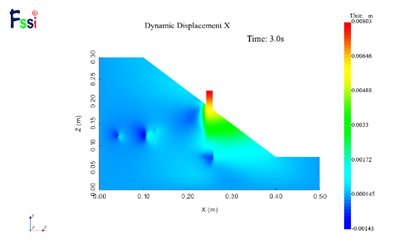
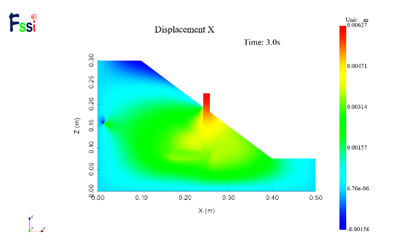
图27正弦地震波作用下水平动位移分布云图
3 结论
本文采用的数值模拟方法及结果在土坡稳定性分析和抗滑桩设计中具有重要的参考价值,特别是在提高边坡稳定性方面,L型抗滑桩显示出显著的优势。具体结论有:
(1) 数值模拟与试验验证:
数值模拟结果与离心模型试验结果在水平位移和竖向位移的分布上基本一致。
两种不同加载方式(直接加载至50g和逐级加载至50g)在模拟中结果相符,证明直接加载至50g的方法具有可信度。
(2) 误差分析:
数值模拟与离心模型试验的位移变化趋势高度相符。
竖向位移误差不超过5%,水平位移误差不超过15%,在可接受范围内,验证了数值模拟的准确性。
(3) 抗滑桩支护效果:
L型抗滑桩比I型抗滑桩显著减少了边坡的水平位移,最大水平位移分别为3.57mm(L型)和5.08mm(I型)。
未加固边坡的水平位移最大值为5.28mm,显示L型抗滑桩对边坡稳定性有显著提升效果。
(4) 地震波作用下的稳定性:
在正弦周期性地震波作用下,L型抗滑桩的最大水平动位移为6.17mm,而I型为10.9mm,表明L型支护的动力边坡稳定性更强。实际地震波(如北岭地震波)作用下,L型抗滑桩的抗倾覆能力更强,进一步验证了其优越性。
参考文献
[1] 张倬元.滑坡防治工程的现状与发展展望[J].地质灾害与环境保护,2000,(02):89-97+181.
[2] Liu S , Luo F , Zhang G .Centrifuge model tests on pile-reinforced slopes subjected to drawdown[J].岩石力学与岩土工程学报:英文版, 2020.
[3] 伞立忠.自升式钻井平台桩靴结构设计[D].大连理工大学,2012.
[4] 赖踊卿.软黏土地基海上风机大直径单桩水平受荷特性与分析模型[J].[2024-06-15].
[5] 彭秀华,刘素嘉,张涵轲,等.L型抗滑桩加固土坡特性的离心模型试验与有限元模拟研究[J].工程地质学报, 2024(001):032.