摘要:进行半圆盘三点弯曲试验,按照与试验相同的方式提取数值模拟试验中相应监测线上的x位移数据,与DIC结果进行比对。发现裂纹尖端感兴趣的区域内位移变化模式完全与试验结果相同,尤其沿竖向监测线分布的位移,横向监测线位移结果与DIC结果相似但不如试验明显,分析原因是因为没有开裂,以上结果表明FssiCAS很好的模拟了裂纹尖端位移场特征和断裂过程区FPZ。将模拟出的FPZ考虑在内,根据国际岩石力学学会建议的方法计算应力强度因子,并计算了x方向的应力解析解,与数值模拟结果相吻合,最靠近裂纹尖端的结点误差越小,距离最近的结点误差仅1.2%。
1 Abaqus建模
本建模过程非本次主要内容且模型简单,不详细赘述。为方便提取数据提取画好结构线,使得划分的网格结点在同一水平或竖直线上,方便分析。并在裂纹尖端处对网络局部加密。(图1)
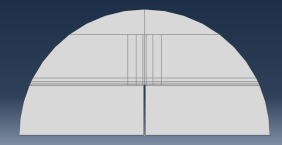
图1 Abaqus建模
2 计算分析过程
2.1导入网格文件.inp
点击FSSI-CAS-2D/3D—Preprocess—Load Mesh—Abaqus,在弹出的文件选择对话框中选择Abaqus输出的网格文件.inp,点击打开按钮。在弹出对话框中设置流体节点阶次,将流体节点阶次设置为0,点击ok按钮确认选择。三点弯试验边界条件简单不需要导入网格线进行辅助。
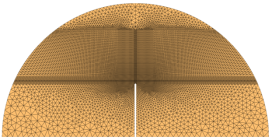
图2 模型导入
2.2设置计算参数
2.2.1 边界条件设置
首先对模型底部两个对称结点上施加纵向的位移约束为0,结点编号分别为1309,1399。在顶部中心结点上施加荷载-100N作为试验预应力荷载,结点编号为54。在裂纹正上方中轴上所有结点施加水平位移约束为0。点击工具栏中Apply Boundary图标,进入相应的点选择模式。点击键盘‘R’键,进行选择,被选中的对象会变亮,通过此操作进行一次设置上述边界。可通过在右侧快捷窗口中点击 Show Boundary Condition,检查是否正确添加边界条件。具体边界条件如下图所示。在step2中导入预设的加载路径,考虑时程的加载,1s时加载到1500N。
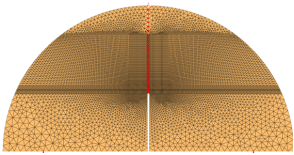
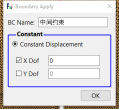
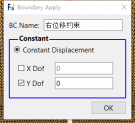
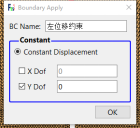
图3 边界条件设置
2.2.2 参数设置
选取第一步计算本构模型为弹性本构模型,具体材料参数参考砂岩的物理参数设置,如下所示。
断裂韧性的计算与半圆盘的厚度密切相关,试验半圆盘厚度为30mm,平面应变问题是一般默认厚度为1,需要对相关材料参数按照厚度比例进行折减,试验测得砂岩弹性模量为2.5Gpa,根据厚度比1:33,将数值模拟弹性模量设置为0.075Gpa
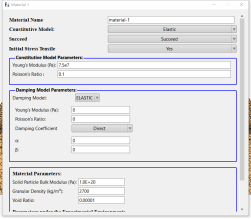
图4 材料参数设置
本实验为静态加载,无水动力、风荷载、地震等动力条件,选择No Hydro、No Earthquake。重力场条件设置如下。

图5 重力场设置
2.2.3 求解器条件设置
点击 FSSI-CAS-2D/3D—Preprocess—Solver—Solver Type,在弹出对话框中设置求解器类型。选择平面应变问题,此后不做修改。
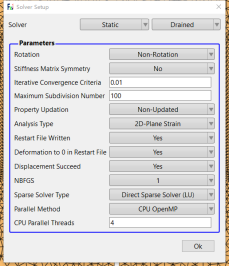
图 6 求解器设置
2.2.4 时间步设置
点击 FssiCAS—Preprocess—Solver—Time Step(以step2为例)。Step 2 的时间步选项卡中 Simulation Time (s)为计算总时间,设置为1 s;Start Time of Current Step(s)为开始计算时间,设置为 0 s;Interval for Time Steps (s)为时间步长,设置为 0.1s;Interval for Updating Coordinate (s)为坐标更新时间,设置为10s;Interval for Updating Global Stiffness Matrix (s)为刚度矩阵更新时间,设置为10s;Maximum lterations 为每个时间步最大迭代次数,设置为 20 步;Restart File Output Interval(s)为输出重启文件的时间,设置为10s;Results File Output Interval (s)为输出某一时刻所有节点/高斯点上的位移、应力、应变等结果文件的时间间隔,设置为每 0.1 s 输出一次结果文件;Results Output 为选择输出节点上结果;State Variables Output 为选择是否输出状态变量;Results Sequence 为选择设置计算结果序列,可选择是否计算保存位移、应力、应变、孔压、渗流速度、渗流力、加速度等结果;Results Format 为计算结果文件形式,可选择保存为二进制文件或 ASCII 文件;History Output Interval (s)为输出特定的节点或单元上的应力、应变等结果文件的时间间隔,设置为每 0.05 s 输出一次。α,β1,β2 为时间系数,保持默认值即可,完成设置后分别点击 Create。设置完成后点击添加时间步,材料属性采用弹性状态计算,设置不同的荷载条件,其他设置不变。设置输出应变云图,具体参数见下图。
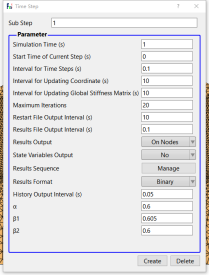
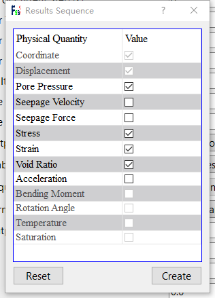
图 7 时间步设置
2.2.5 监测点设置
为方便提取位移和应变数据,参考DIC提取数据的方式,设置计算过程中的监测点,用于提取具体的数据数值进行对此观测,监测点设置范围为裂纹尖端一定范围内,因为是在有限元计算框架内,为求结果的准确性,根据线弹性断裂力学要求,所提取的数据点不应离裂纹尖端过远,尤其用于应力对比的点位。同时,提取的众多结点满足x坐标相同或者y坐标相同。依据上述要求,具体结点位置见下图和附件。
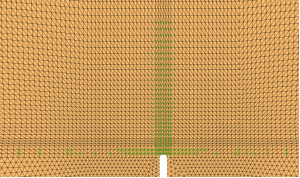
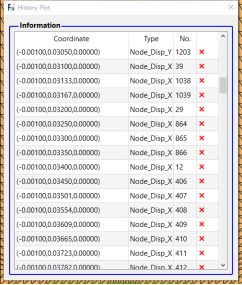
图8 监测点位置及部分坐标
2.3 各时间步加载条件设置
在第一个加载步中设置预加载-100N,第二步中导入预先写好的时程加载文件。并设置初始条件,在 Step 1 时间步操作界面中点击 FSSI-CAS-2D/3D—Preprocess—Initial State,设置初始条件,点击 ok,完成初始状态设置。
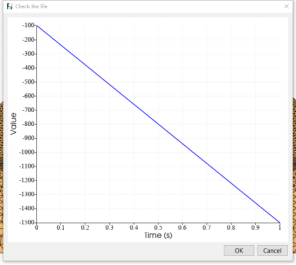
图9 初始条件与第2步荷载展示
2.9 计算
点击 FSSI-CAS-2D/3D—Preprocess—Computation—FSSI-W,选择All step进行计算,保存当前项目到目标文件夹,开始计算,等待计算结束后,关闭计算页面。
图 10 计算结束页面
3 后处理
3.1加载文件
点击 FSSI-CAS-2D/3D—Postprocess—Open Results File,选择需要处理的结果文件夹,点击Open Result Files,选择文件夹导入结果文件,进行后处理。
3.2云图绘制
点击Displacement、Effective stress等进行云图绘制,以1500N为例展示结果。
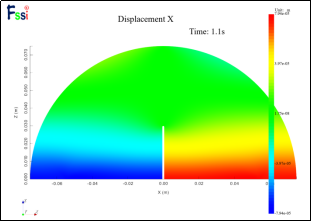
图 11 1500N x方向位移云图
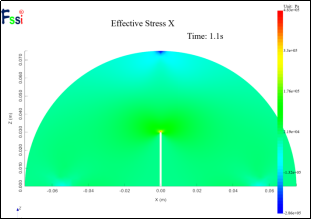
图 12 1500N x方向应力云图
4数据提取
4.1 应力-位移数据模拟与试验结果对比
1500N时的位移约为0.142mm,试验中线弹性段直到1500N时的位移平均值在0.115mm,试验中试样的离散性较大,考虑到弹性模量不精确,认为试验结果在可接受范围内。试验结果见本文档任务简介2。
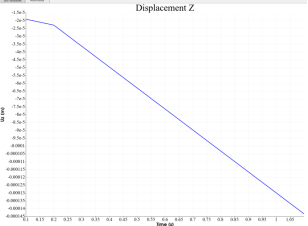
图13 施加荷载点(点54)的位移变化
4.2 确定监测点与监测线
首先根据Time History中记录的监测点编号和坐标进行统计,统计line1、line、 line3、line4、line5、line6的结点编号,统计第1500N对应的x方向位移和x方向应力。如下图所示。其中line1、line、 line3、line4的x轴坐标分别为-0.001,-0.00033,0.00033,0.0001,line5、line6的横坐标分别为0.0005,0。各结点处的位移数据见下图
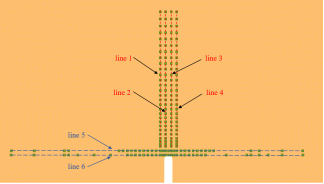
图14 提取的定位点
4.3 FPZ尖端确定
图14中line2与line3中最下方的两个结点离裂纹位置极近,可以认为是裂纹起裂的临界状态。由图16e可知,当沿竖向上位移近似为0或斜率基本不变时即为FPZ的终点。
对模拟数据按图16e所示方式提取数据并绘图,如图17可见。当y=2mm时,位移变化斜率增大到一定值且变化很小,y>2mm的点处x方向位移变化很小,认为FPZ的长度为2mm。当y处于0-2mm时,位移快速减小,呈现与图16e相同的趋势,可以认为模型很好的反应了裂纹尖端FPZ的特点,长度约为2mm。对比图16e中y=5.25mm(对应的裂纹尖端,红线标注)是裂纹两侧的张开位移约为3um,数值模拟均值为3um,基本相同。
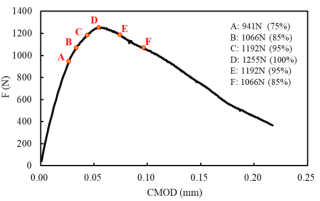
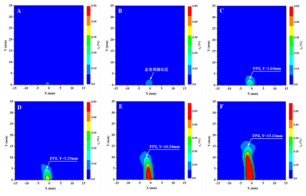
图15 断裂过程区发展过程[2]
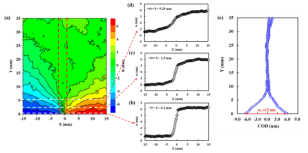
图16 DIC位移提取数据(峰值时刻)[2]
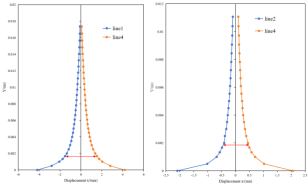
图 17 沿竖向分布线x向位移变化过程
图18为x方向位移沿line5、line6的变化过程,在-22mm直接位移变化斜率明显增大,与图15b、c、d中所示趋势类似,呈现出裂纹尖端断裂过程区FPZ内的位移分布特点,可以认为水平-22mm范围为FPZ区域。
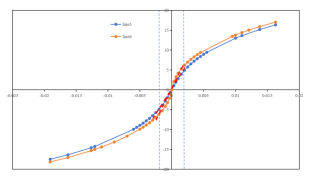
图 18 沿横向分布线x向位移变化过程
结合图19中裂纹尖端位移分布云图,尽管由于颜色条设置原因无法将位移分布离散成多个区域,但仍可以发现位移等势线相交于裂纹尖端,与图16a中的DIC表面变形观测一致。结合以上数据,认为计算结果很好的模拟了裂纹起裂断裂过程区的发展变化和特点。可以预见若用合适的后处理软件,将达到与图16a中相同的效果。
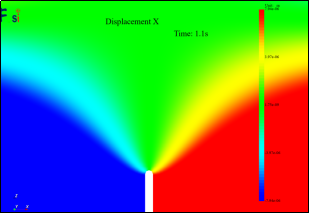
图 19裂纹尖端位移分布云图
4.4裂纹尖端局部化区域应力场计算
准确求解应力强度因子的关键是找到FPZ的长度,根据国际岩石学会建议的方法计算Ⅰ型应力强度因子,计算公式为:
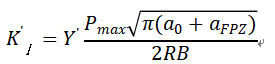
a为裂纹长度、aFPZ为断裂过程区长度,R为半圆盘半径,B为半圆盘厚度,
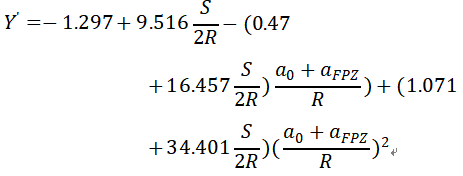
上式为考虑模拟中FPZ以后的修正计算公式[2],用以验证FPZ准确性及是否与解析解吻合
因为计算的问题为平面应变问题,试样厚度默认为1。按下图20所示,在裂纹尖端局部化范围内选取两个测点进行水平方向应力计算。测点的坐标为1(0.00025,0),2(0,-0.00033)。注:断裂力学中通常认为裂纹延伸方向为x方向,所以与Fssi中坐标方向相反,模拟中x方向应力应为。线弹性断裂力学中应力解析解计算公式如下:
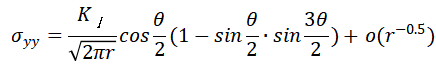
其中,r为距离裂纹尖端的距离,为倾角,计算得到1点401497.5898Pa,2点=399840.782Pa,因为1点处于上下两结点中间位置,通过取上下两点的应力的平均值作为1点应力,Pa,2点应力394552Pa。由以上对比得模拟计算应力结果与理论计算结果相差不大,1点误差在2.2%,因为距离裂纹越远数值偏差越大,受距离裂纹尖端位置较远结点的影响,2点误差则很小为1.2%,其中在计算2点应力时,选择2点到裂纹的垂直距离来计算应力,垂直距离约为0.000126(如图20)。
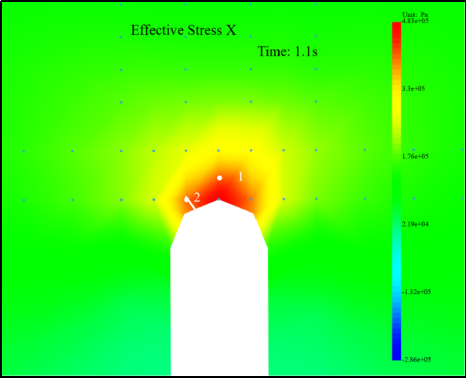
图20 裂纹尖端应力局部化云图
参考文献:
[1] KURUPPU M D, OBARA Y, AYATOLLAHI M R, et al. ISRM-Suggested Method for Determining the Mode I Static Fracture Toughness Using Semi-Circular Bend Specimen[J]. Rock
Mechanics and Rock Engineering, 2013, 47(1): 267-274.
[2]Shuting M ,Zhi P P ,Wenbo H , et al.Determination of mode I fracture toughness of rocks with field fitting and J-integral methods[J].Theoretical and Applied Fracture Mechanics,2022,(prepublish):103263-.